Chapter - 5

Key Words: Overview, Compressors, Ratio, Attack, Gain

Impulse Signal

🎯 Learning Objectives

By the end of this topic, you should be able to:

  • Understand what an impulse signal is in discrete-time DSP
  • Explain the difference between a continuous-time Dirac delta and discrete-time impulse
  • Recognize why the impulse plays a key role in system analysis
  • Describe how the impulse is used to compute convolution and impulse response
  • Generate and visualize impulse signals in discrete-time

Impulse Signal:

This is an Impulse signal as shown in the figure below. It is made up of a single sampled value of one in an infinitely long stream of zeros. You can think about it as a burst of energy which arrives really quickly and dissipates just as quickly.

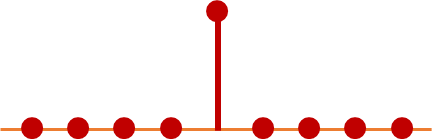
Signal domain illustration
Figure.

Suffice to say a one sample burst of energy does not actually occur naturally but it can be generated via code a comparable example to an Impulse would be clubbing your hand or bursting a balloon a very profound thing about this impulse signal is that this simple signal this tiny one sample poles contains sinusoids of all possible frequencies representable for that sampling rate. This may be difficult to appreciate and certainly hard to grasp but it practically contains all possible frequencies because of this property the impulse signal is very useful in systems analysis.

In discrete-time DSP, the impulse signal is defined as:

δ[n]={1,n=00,n≠0\delta[n] =\begin{cases}1, & n = 0 \\0, & n \ne 0\end{cases}

Impulse is the “Identity Input” of LTI Systems

For any LTI system:

y[n]=x[n]∗h[n]y[n] = x[n] * h[n]

If we input an impulse:

x[n]=δ[n]x[n] = \delta[n]

Then:

y[n]=h[n]y[n] = h[n]

This is why:

The impulse response completely characterizes an LTI system.

Properties of the Impulse Signal

  • Sampling property:
    x[n] δ[n−n0]=x[n0]x[n] \, \delta[n - n_0] = x[n_0]
  • Shifting:
δ[n−n0]=1 at n=n0\delta[n - n_0] = 1 \text{ at } n = n_0
  • Convolution identity:
x[n]∗δ[n]=x[n]x[n] * \delta[n] = x[n]
  • System response extractor
    Feeding an impulse reveals the system’s impulse response.

Exercise:

Let us actually create an Impulse signal and put its wild claim to the test we are going to use Python to create a test signal. The exercise is available below in python sandbox

Exercise Video
Wahtch the video for help

Press Run Code: Output will appear here.

SINC Function and Impulse Signal:

Demonstration Video

Impulse Signal in Audio DSP:

Although a true 1-sample spike can be harsh in audio, it is often used to:

  • Measure room impulse responses
  • Generate convolution reverbs
  • Analyze systems like speakers or microphones
  • Extract IRs for EQ or amplifier modeling

🎨 Interactive Test Signal & Filter Demo

🎛 Interactive Impulse Generator

Enable multiple impulses

This generator produces a **discrete-time impulse train**, perfect for testing: FIR filters, IIR responses, convolution logic, and time-domain analysis.

FIR Filter Coefficients

Time Domain

Blue: Input, Red: Output

FFT Magnitude

Green: Magnitude

Phase Response

Orange: Phase (normalized)

🧠 Key Takeaways

  • The discrete-time impulse is 1 at n=0 and 0 elsewhere.
  • It is the most fundamental building block in DSP.
  • Feeding an impulse to an LTI system gives the impulse response.
  • The impulse response determines the complete behavior of the system.
  • Convolution with the impulse leaves a signal unchanged.

🧠 Quick Quiz

Test your understanding of feedforward filters:

1) What is the value of δ[n] when n ≠ 0?

2) What output does an LTI system produce when the input is δ[n]?

3) The impulse δ[n] is also known as:

4) Convolution of x[n] with δ[n] results in:

5) What happens when the impulse is shifted, δ[n – 5]?