Chapter - 10

Key Words: Sound sources, Spherical waves, Monopole, Dipole, Radiation, Acoustics

Spherical Harmonics

🎯 Learning Objectives

By the end of this topic, you should be able to:

  • Describe and mathematically model monopole, dipole, and distributed sources.
  • Derive the spherical wave solution of the acoustic wave equation.
  • Understand volume velocity, sound power, and radiation impedance.
  • Calculate directivity factors and far-field sound pressure levels.
  • Apply these principles to practical sound source characterization and simulation.

Spherical Harmonics and Plane Waves:

Starting with the Laplace operator, we obtain a separable solution:

p=Ψ(r,θ,ϕ)ejωt=R(r) P(θ) Φ(ϕ) ejωtp = \Psi(r,\theta,\phi)e^{j\omega t} = R(r)\,P(\theta)\,\Phi(\phi)\,e^{j\omega t}

which leads to three differential equations including three constants mm, CC, and kk.

(∂2∂ϕ2+m2)Φ=0(\frac{\partial^2}{\partial\phi^2} + m^2)\Phi = 0
1sin⁡θ∂∂θ+(C−m2sin⁡2θ)P=0\frac{1}{\sin\theta}\frac{\partial}{\partial\theta} + \left(C - \frac{m^2}{\sin^2\theta}\right)P = 0
1r2∂∂r(r2∂R∂r)+(k2−Cr2)R=0\frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2\frac{\partial R}{\partial r}\right) + \left(k^2 - \frac{C}{r^2}\right) R = 0

The solution for the azimuth angle is:

Φ=ejmϕ\Phi = e^{j m \phi}

For the elevation angle θ\theta, the orthonormal Legendre polynomials of degree mm and order nn complete the spatial angular solution:

Pnm(x)=(−1)m(1−x2)m/2dmdxmPn(x),0≤m≤nP_n^m(x) = (-1)^m (1 - x^2)^{m/2} \frac{d^m}{dx^m} P_n(x), \quad 0 \le m \le n
Pn−m(x)=(−1)m(n−m)!(n+m)!Pnm(x)P_n^{-m}(x) = (-1)^m \frac{(n-m)!}{(n+m)!} P_n^m(x)

with the standard Legendre polynomial

Pn(x)=12nn!dndxn(x2−1)nP_n(x)=\frac{1}{2^n} n! \frac{d^n}{dx^n}(x^2 - 1)^n

Thus, the angular part becomes the spherical harmonic:

Ynm(θ,ϕ)=2n+14π(n−m)!(n+m)! Pnm(cos⁡θ)ejmϕY_n^m(\theta,\phi)=\sqrt{\frac{2n+1}{4\pi}\frac{(n-m)!}{(n+m)!}}\, P_n^m(\cos\theta)e^{jm\phi}

Negative–order harmonics follow from:

Ynm(θ,ϕ)=(−1)m Yn−m∗(θ,ϕ)Y_n^m(\theta,\phi) = (-1)^m\, Y_n^{-m*}(\theta,\phi)

Spherical harmonics serve as an orthonormal basis over the surface of the unit sphere.

Radial Solutions and Near-Field Behavior:

With near-field effects included, the radial equation becomes

1r2∂∂r(r2∂R∂r)+k2R+n(n+1)r2R=0\frac{1}{r^2}\frac{\partial}{\partial r}(r^2\frac{\partial R}{\partial r}) + k^2 R + \frac{n(n+1)}{r^2} R = 0

Its solutions are spherical Hankel functions:

R(r)=hn(1)(kr)+hn(2)(kr)R(r) = h_n^{(1)}(kr) + h_n^{(2)}(kr)

Thus the full spherical mode is:

Ψnm(k,r,θ,ϕ)=(hn(1)(kr)+hn(2)(kr))Pnm(cos⁡θ)ejmϕ\Psi_n^m(k,r,\theta,\phi)=\left(h_n^{(1)}(kr)+h_n^{(2)}(kr)\right) P_n^m(\cos\theta) e^{jm\phi}

Modes are orthogonal over the sphere:
Spherical harmonics can be used to decompose measured or simulated source directivities.

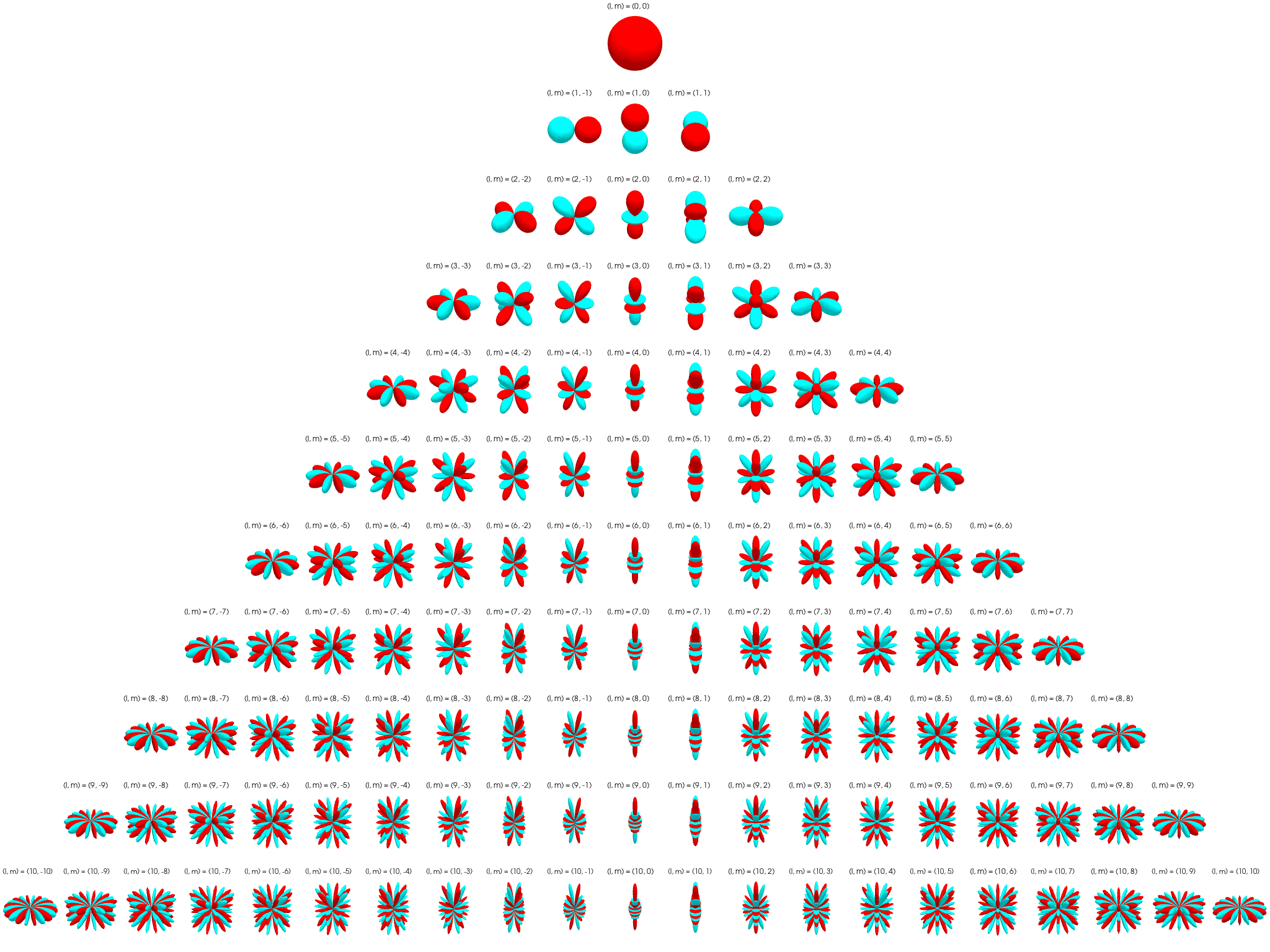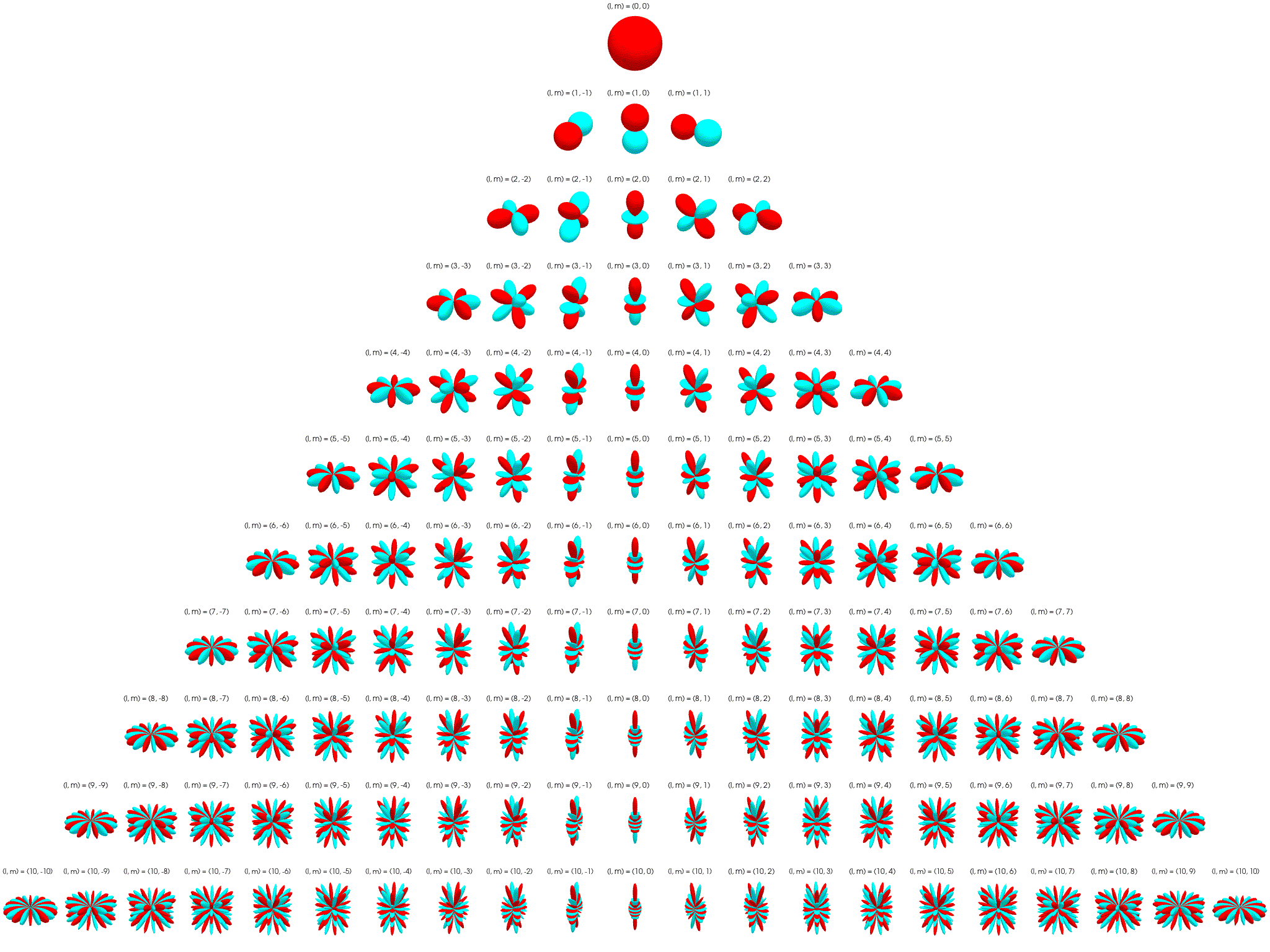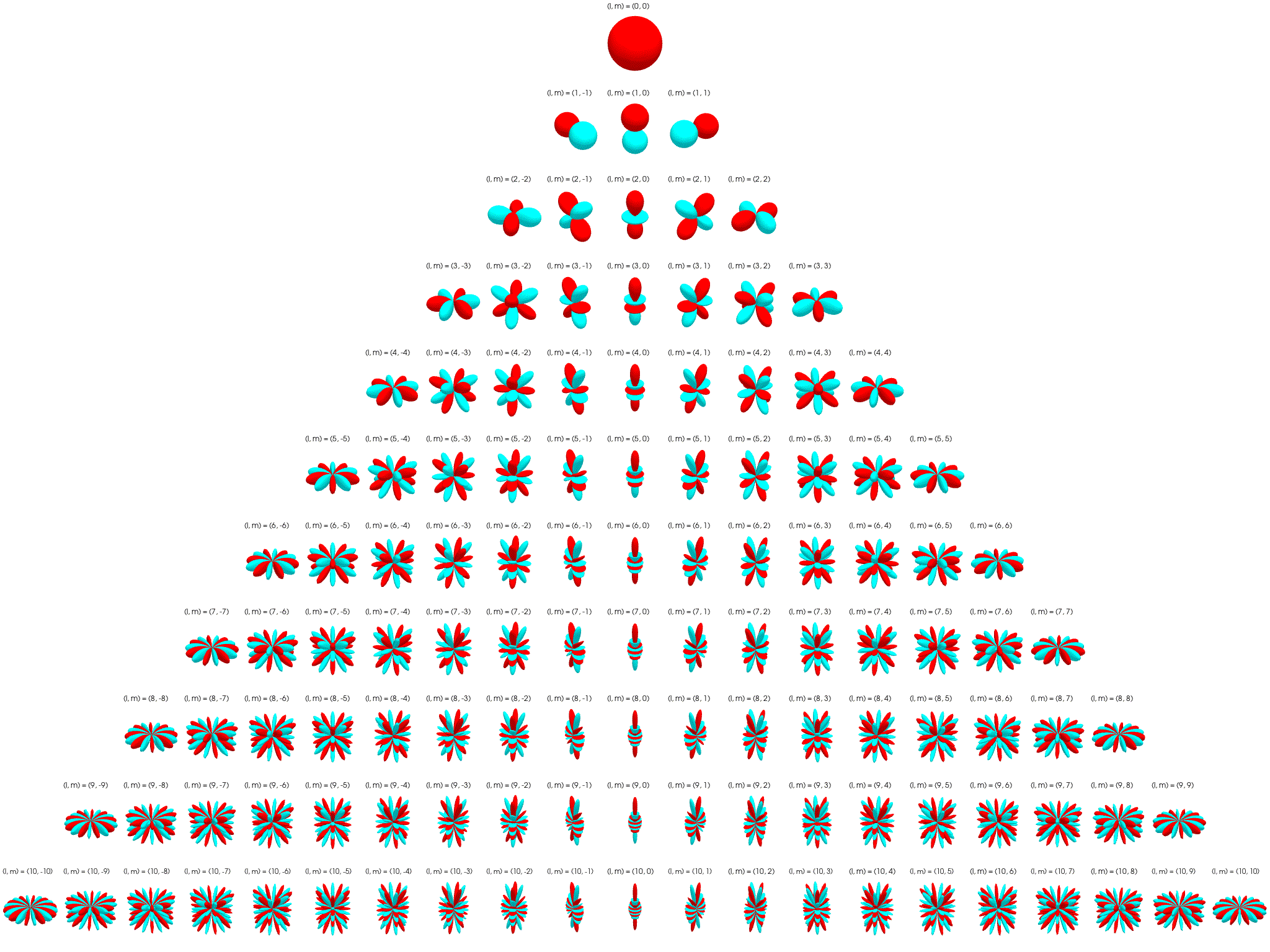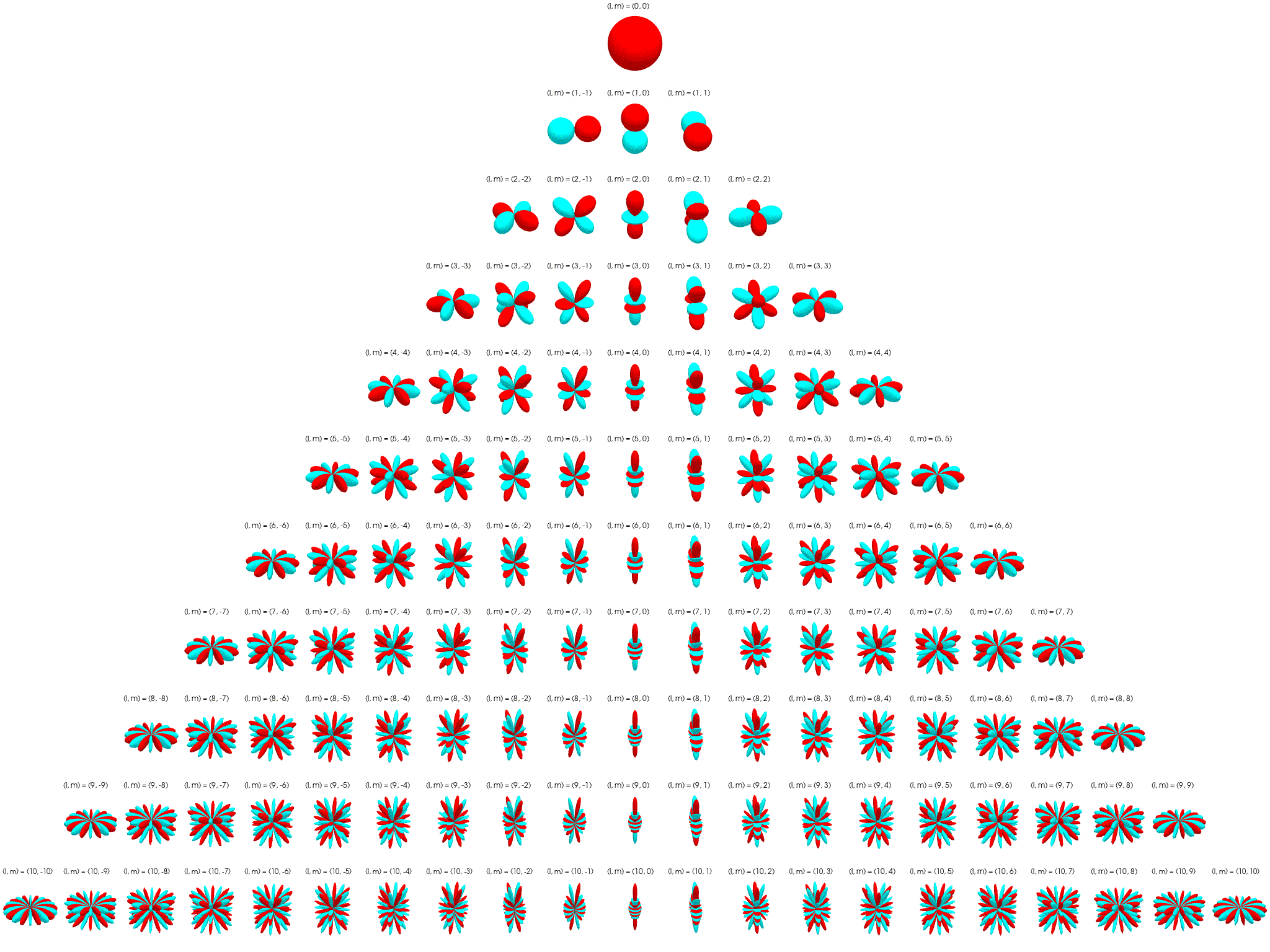
Dipole radiation

Figure. Dipole source radiation pattern.

Spherical Harmonics (SH) Transformation:

Any function f(θ,ϕ)f(\theta,\phi) can be expanded:

f(θ,ϕ)=∑n=0∞∑m=−nnfnmYnm(θ,ϕ)f(\theta,\phi) = \sum_{n=0}^{\infty}\sum_{m=-n}^{n} f_{nm} Y_n^m(\theta,\phi)

Coefficients are obtained via

fnm=∫02π∫0πf(θ,ϕ) Ynm∗(θ,ϕ) sin⁡θ dθ dϕf_{nm} = \int_{0}^{2\pi}\int_{0}^{\pi} f(\theta,\phi)\, Y_n^{m*}(\theta,\phi)\, \sin\theta\, d\theta\, d\phi

This is analogous to Fourier series on a sphere.
If fnmf_{nm} represents outgoing modes, the pressure field is

pnm(k,r)=fnm(k) hn(2)(kr)p_{nm}(k,r) = f_{nm}(k)\, h_n^{(2)}(kr)

Plane Wave Representation with Spherical Harmonics:

A plane wave decomposes into spherical harmonics:

p(r,k,θ,ϕ)=4π∑n=0∞injn(kr)∑m=−nnYnm(θ,ϕ) Ynm∗(θp,ϕp)p(r,k,\theta,\phi) = 4\pi \sum_{n=0}^{\infty} i^n j_n(kr) \sum_{m=-n}^{n} Y_n^m(\theta,\phi)\, Y_n^{m*}(\theta_p,\phi_p)

This relationship forms the theoretical foundation of Ambisonics and spatial audio rendering.

Multipole Synthesis:

Multipoles approximate source directivity by superposition of:

  • Monopoles
  • Dipoles
  • Quadrupoles
  • Higher-order poles

Differences:

  • SH: centered at a single point, global basis
  • Multipoles: spatially placed, often more efficient for non-spherical sources
  • Multipoles converge faster when a source does not exhibit spherical symmetry.

🧪 Interactive Examples

Spherical Harmonic Visualizer

📝 Key Takeaways

  • Spherical harmonics form an orthonormal basis on the sphere for directional acoustic fields.
  • Directivities and radiation patterns can be encoded, analyzed, and reconstructed using SH coefficients.
  • The radial dependence of modes is governed by spherical Hankel functions, capturing near- and far-field behavior.
  • Plane waves can be expanded into SH, enabling sound field synthesis (e.g., higher-order Ambisonics).
  • Multipole expansions offer an alternative to SH for modeling non-spherical or complex sources with fewer parameters.

🧠 Quick Quiz

1) Which function forms the angular basis for decomposing a directional acoustic fieldf(θ,ϕ)f(\theta,\phi)?

2) The radial dependence of a spherical wave is described by which functions?

3) A plane wave expansion in SH is essential for which technology?