Chapter - 5

Key Words: Overview, Compressors, Ratio, Attack, Gain

Infinite Impulse Response

šŸŽÆ Learning Objectives

By the end of this topic, you should be able to:

  • Understand why some filters have an impulse response that lasts forever.
  • Explain the role of feedback in generating infinite impulse responses.
  • Write and interpret the difference equation of a basic IIR filter.
  • Visualize the impulse response of an IIR filter in Python.
  • Understand stability conditions of recursive digital filters.

Infinite Impulse Response (IIR):

In the previous topics, we learned that FIR filters (Finite Impulse Response) have an impulse response that eventually goes to zero after a finite number of samples.
Now we consider the second major class of digital filters:

Infinite Impulse Response (IIR) filters - filters whose impulse response theoretically continues forever.

These filters arise whenever the output depends not only on past input samples but also on past output samples.
This introduces recursion, creating an impulse response that decays but never fully reaches zero.

What Makes an IIR Filter "Infinite"?

Let us consider a simple recursive filter given by:

y[n]=x[n]+aā€‰y[nāˆ’1]y[n] = x[n] + a\,y[n-1]

This filter feeds a portion of the output back into itself.
This small change drastically alters the impulse response.

If the input is an impulse:

x[0]=1,x[n>0]=0x[0] = 1,\quad x[n>0] = 0

Then the output becomes:

y[0]=1y[1]=ay[2]=a2y[3]=a3y[0] = 1 \\y[1] = a \\y[2] = a^2 \\y[3] = a^3

This continues forever (mathematically).
If āˆ£aāˆ£<1|a| < 1, these values decay, but they never fully reach zero.

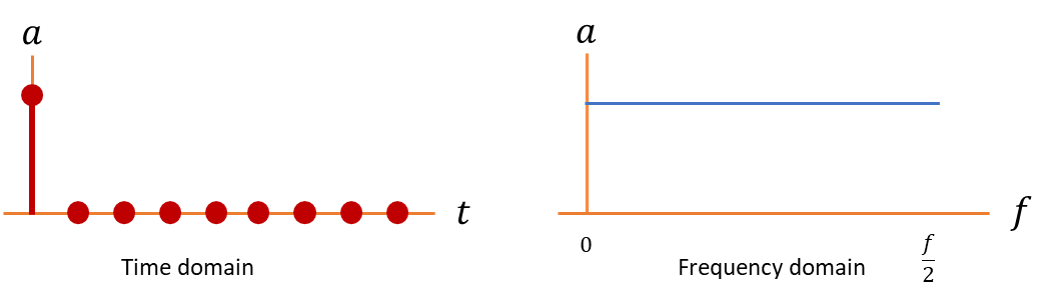
IIR feedback diagram
Figure. Recursive feedback path creates an infinite impulse response.

Stability of IIR Filters:

Because IIR filters have feedback, they can become unstable.

  • If āˆ£aāˆ£<1|a| < 1"
    impulse response decays ā†’ stable
  • If āˆ£aāˆ£=1|a| = 1:
    impulse response persists ā†’ marginally stable
  • If āˆ£aāˆ£>1|a| > 1:
    impulse response grows without bound ā†’ unstable

We normally require:

āˆ£aāˆ£<1|a| < 1

to construct stable IIR filters.

Python Example

Press Run Code: Output will appear here.

Why IIR Filters Are Important:

Even though they introduce recursion, IIR filters offer several advantages:
āœ” More efficient
A well-designed IIR filter can approximate an analog filter with far fewer coefficients than an FIR filter. āœ” Better frequency selectivity
IIR filters can achieve sharp transitions using fewer taps. āœ” Classical filter families
Butterworth, Chebyshev, and Elliptic filters are implemented as IIR filters.

However, the tradeoff is:

  • Potential instability
  • Non-linear phase
  • More difficult to design

šŸŽØ Interactive Test Signal & Filter Demo

IIR Filter Interactive Demo

Key Takeaways

  • IIR filters have feedback, making their impulse response theoretically infinite.
  • A simple recursion like ( y[n] = x[n] + a,y[n-1] ) produces a decaying exponential response.
  • For stability, feedback coefficients must satisfy ( |a| < 1 ).
  • IIR filters can achieve sharp frequency responses using fewer coefficients than FIR filters.
  • They are widely used in classical filter design (Butterworth, Chebyshev, etc.).

šŸ§  Quick Quiz

Test your understanding of IIR filters:

1) What causes an impulse response to be infinite in an IIR filter?

2) What condition ensures stability for a simple recursive filter y[n] = x[n] + a y[nāˆ’1]?

3) If |a| > 1 in an IIR filter, what happens?

4) Compared to FIR filters, IIR filters usually require:

5) Which of the following is a classical IIR filter family?